机器学习核心公式全攻略

Chuck Chen

· 2025年5月30日

来源

本文翻译自The Most Important Machine Learning Equations: A Comprehensive Guide。

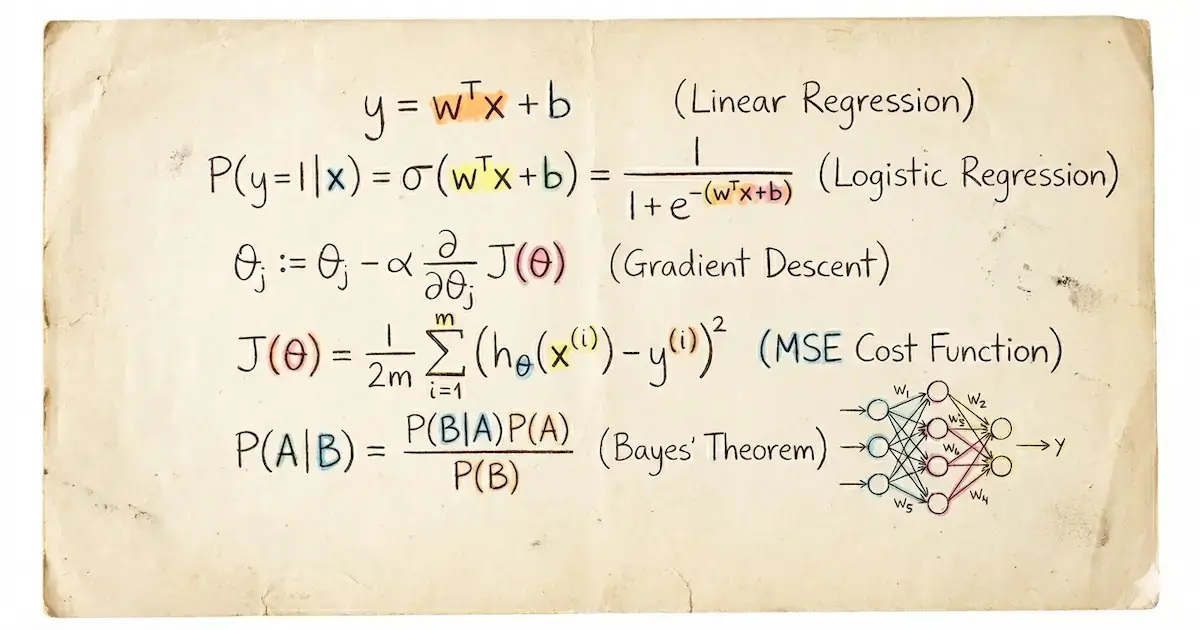
动机

机器学习（ML）是一个由数学驱动的强大领域。无论你是正在构建模型、优化算法，还是仅仅想理解机器学习底层的运作机制，掌握核心公式都是至关重要的。这篇博文旨在成为你的首选资源，涵盖了最关键且最具“震撼力”的机器学习公式——足以让你掌握机器学习背后的大部分核心数学知识。每个部分都包含理论洞察、公式本身以及 Python 中的实践实现，以便你能看到数学的实际应用。

本指南适用于任何具有基本数学和编程背景、并希望深入理解机器学习的人。

简介

数学是机器学习的语言。从概率到线性代数，从优化到高级生成模型，公式定义了机器学习算法如何从数据中学习并做出预测。本博文汇集了最基本的公式，解释了它们的重要性，并提供了使用 NumPy、scikit-learn、TensorFlow 和 PyTorch 等 Python 库的实践示例。无论你是初学者还是资深从业者，本指南都将为你提供有效理解和应用机器学习数学的工具。

概率与信息论

概率论和信息论为推理不确定性和衡量分布之间的差异提供了基础。

贝叶斯定理

公式：

P(A|B) = \frac{P(B|A) P(A)}{P(B)}

说明： 贝叶斯定理描述了在给定新证据（ $B$ ）的情况下如何更新假设（ $A$ ）的概率。它是概率推理的基石，广泛用于分类和推理等机器学习任务。

实际应用： 应用于朴素贝叶斯分类器、贝叶斯网络和贝叶斯优化。

代码实现：

def bayes_theorem(p_d, p_t_given_d, p_t_given_not_d):
    """
    使用贝叶斯定理计算 P(D|T+)。
 
    参数:
    p_d: P(D)，患病的概率
    p_t_given_d: P(T+|D)，患病时检测呈阳性的概率
    p_t_given_not_d: P(T+|D')，未患病时检测呈阳性的概率
 
    返回:
    P(D|T+)，检测呈阳性时患病的概率
    """
    p_not_d = 1 - p_d
    p_t = p_t_given_d * p_d + p_t_given_not_d * p_not_d
    p_d_given_t = (p_t_given_d * p_d) / p_t
    return p_d_given_t
 
# 示例用法
p_d = 0.01  # 人口中有 1% 患病
p_t_given_d = 0.99  # 检测灵敏度为 99%
p_t_given_not_d = 0.02  # 检测的假阳性率为 2%
result = bayes_theorem(p_d, p_t_given_d, p_t_given_not_d)
print(f"P(D|T+) = {result:.4f}")  # 输出: P(D|T+) = 0.3333

熵 (Entropy)

公式：

H(X) = -\sum_{x \in X} P(x) \log P(x)

说明： 熵衡量概率分布中的不确定性或随机性。它量化了描述该分布所需的信息量，是理解信息增益和决策树等概念的基础。

实际应用： 用于决策树、信息增益计算，以及作为其他信息论指标的基础。

代码实现：

import numpy as np
 
def entropy(p):
    """
    计算概率分布的熵。
 
    参数:
    p: 概率分布数组
 
    返回:
    熵值
    """
    return -np.sum(p * np.log(p, where=p > 0))
 
# 示例用法
fair_coin = np.array([0.5, 0.5])  # 公平硬币正反面概率相同
print(f"公平硬币的熵: {entropy(fair_coin)}")  # 输出: 0.6931471805599453
 
biased_coin = np.array([0.9, 0.1])  # 偏向硬币正面概率更高
print(f"偏向硬币的熵: {entropy(biased_coin)}")  # 输出: 0.4698716731013394

联合概率与条件概率

公式：

联合概率： $P(A, B) = P(A|B) P(B) = P(B|A) P(A)$
条件概率： $P(A|B) = \frac{P(A, B)}{P(B)}$

说明： 联合概率描述了两个事件同时发生的可能性，而条件概率衡量了在给定另一个事件的情况下一个事件发生的概率。这些是贝叶斯方法和概率图模型的基础。

实际应用： 用于朴素贝叶斯分类器和概率图模型。

代码实现：

from sklearn.naive_bayes import GaussianNB
import numpy as np
 
# 使用 GaussianNB 演示条件概率在分类中的应用
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])
model = GaussianNB().fit(X, y)
print(model.predict([[2.5, 3.5]]))  # 输出: [1]

KL 散度 (Kullback-Leibler Divergence)

公式：

D_{KL}(P \| Q) = \sum_{x \in \mathcal{X}} P(x) \log \left( \frac{P(x)}{Q(x)} \right)

说明： KL 散度衡量一个概率分布 $P$ 与另一个分布 $Q$ 的偏离程度。它是非对称的，是信息论和生成模型的基础。

实际应用： 用于变分自编码器 (VAE) 和模型评估。

代码实现：

import numpy as np
 
P = np.array([0.7, 0.3])
Q = np.array([0.5, 0.5])
kl_div = np.sum(P * np.log(P / Q))
print(f"KL 散度: {kl_div}")  # 输出: 0.08228287850505156

交叉熵 (Cross-Entropy)

公式：

H(P, Q) = -\sum_{x \in \mathcal{X}} P(x) \log Q(x)

说明： 交叉熵量化了真实分布 $P$ 与预测分布 $Q$ 之间的差异。它在分类任务中是一种广泛使用的损失函数。

实际应用： 驱动逻辑回归和神经网络的训练。

代码实现：

import numpy as np
 
y_true = np.array([1, 0, 1])
y_pred = np.array([0.9, 0.1, 0.8])
# 计算二元交叉熵
cross_entropy = -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
print(f"交叉熵: {cross_entropy}")  # 输出: 0.164252033486018

线性代数

线性代数驱动了机器学习模型中的变换和结构。

线性变换

公式：

y = Ax + b \quad \text{其中 } A \in \mathbb{R}^{m \times n}, x \in \mathbb{R}^n, y \in \mathbb{R}^m, b \in \mathbb{R}^m

说明： 该方程表示通过矩阵 $A$ 和偏置 $b$ 将输入 $x$ 线性映射到输出 $y$ 。它是神经网络层中的核心操作。

实际应用： 线性回归和神经网络的基础。

代码实现：

import numpy as np
 
A = np.array([[2, 1], [1, 3]])
x = np.array([1, 2])
b = np.array([0, 1])
y = A @ x + b
print(y)  # 输出: [4 7]

特征值与特征向量

公式：

Av = \lambda v \quad \text{其中 } \lambda \in \mathbb{R}, v \in \mathbb{R}^n, v \neq 0

说明： 特征值 $\lambda$ 和特征向量 $v$ 描述了矩阵 $A$ 如何缩放和旋转空间，对于理解数据方差至关重要。

实际应用： 用于主成分分析 (PCA)。

代码实现：

import numpy as np
 
A = np.array([[4, 2], [1, 3]])
eigenvalues, eigenvectors = np.linalg.eig(A)
print(f"特征值: {eigenvalues}")
print(f"特征向量:\n{eigenvectors}")

奇异值分解 (SVD)

公式：

A = U \Sigma V^T

说明： SVD 将矩阵 $A$ 分解为正交矩阵 $U$ 和 $V$ 以及奇异值的对角矩阵 $\Sigma$ 。它揭示了数据的内在结构。

实际应用： 应用于降维和推荐系统。

代码实现：

import numpy as np
 
A = np.array([[1, 2], [3, 4], [5, 6]])
U, S, Vt = np.linalg.svd(A)
print(f"U:\n{U}\nS: {S}\nVt:\n{Vt}")

优化

优化是机器学习模型从数据中学习的方式。

梯度下降

公式：

\theta_{t+1} = \theta_t - \eta \nabla_{\theta} L(\theta)

说明： 梯度下降通过向损失函数 $L$ 梯度的反方向移动来更新参数 $\theta$ ，移动步长由学习率 $\eta$ 缩放。

实际应用： 训练大多数机器学习模型的支柱。

代码实现：

import numpy as np
 
def gradient_descent(X, y, lr=0.01, epochs=1000):
    m, n = X.shape
    theta = np.zeros(n)
    for _ in range(epochs):
        gradient = (1/m) * X.T @ (X @ theta - y)
        theta -= lr * gradient
    return theta
 
X = np.array([[1, 1], [1, 2], [1, 3]])
y = np.array([1, 2, 3])
theta = gradient_descent(X, y)
print(theta)  # 输出: ~[0., 1.]

反向传播

公式：

\frac{\partial L}{\partial w_{ij}} = \frac{\partial L}{\partial a_j} \cdot \frac{\partial a_j}{\partial z_j} \cdot \frac{\partial z_j}{\partial w_{ij}}

说明： 反向传播应用链式法则来计算神经网络中损失 $L$ 对权重 $w_{ij}$ 的梯度。

实际应用： 实现深度网络的高效训练。

代码实现：

import torch
import torch.nn as nn
 
# 使用 PyTorch 演示自动微分/反向传播
model = nn.Sequential(nn.Linear(2, 1), nn.Sigmoid())
loss_fn = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
 
X = torch.tensor([[0., 0.], [1., 1.]], dtype=torch.float32)
y = torch.tensor([[0.], [1.]], dtype=torch.float32)
 
optimizer.zero_grad()
output = model(X)
loss = loss_fn(output, y)
loss.backward()  # 这会执行反向传播
optimizer.step()
print(f"Loss: {loss.item()}")

损失函数

损失函数衡量模型性能并指导优化。

均方误差 (MSE)

公式：

\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2

说明： MSE 计算真实值 $y_i$ 与预测值 $\hat{y}_i$ 之间差值的平方的平均值，对较大的误差给予更重的惩罚。

实际应用： 回归任务中非常常见。

代码实现：

import numpy as np
 
y_true = np.array([1, 2, 3])
y_pred = np.array([1.1, 1.9, 3.2])
mse = np.mean((y_true - y_pred)**2)
print(f"MSE: {mse}")  # 输出: 0.01

交叉熵损失

（详情参见上文中的“交叉熵”部分。）

高级机器学习概念

这些公式驱动着尖端的机器学习技术。

扩散过程 (Diffusion Process)

公式：

x_t = \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon \quad \text{其中} \quad \epsilon \sim \mathcal{N}(0, I)

说明： 这描述了一个前向扩散过程，其中数据 $x_0$ 随时间 $t$ 逐渐加入噪声，这是扩散模型的一个关键思想。

实际应用： 用于生成式 AI，如图像合成（Stable Diffusion 等）。

代码实现：

import torch
 
x_0 = torch.tensor([1.0])
alpha_t = 0.9
noise = torch.randn_like(x_0)
x_t = torch.sqrt(torch.tensor(alpha_t)) * x_0 + torch.sqrt(torch.tensor(1 - alpha_t)) * noise
print(f"x_t: {x_t}")

卷积运算 (Convolution Operation)

公式：

(f * g)(t) = \int f(\tau) g(t - \tau) \, d\tau

说明： 卷积通过将一个函数滑动到另一个函数上来结合它们，提取图像等数据中的特征。

实际应用： 卷积神经网络 (CNN) 的核心。

代码实现：

import torch
import torch.nn as nn
 
conv = nn.Conv2d(1, 1, kernel_size=3)
image = torch.randn(1, 1, 28, 28)
output = conv(image)
print(output.shape)  # 输出: torch.Size([1, 1, 26, 26])

Softmax 函数

公式：

\sigma(z_i) = \frac{e^{z_i}}{\sum_j e^{z_j}}

说明： Softmax 将原始分数 $z_i$ 转换为概率，总和为 1，非常适合多类别分类。

实际应用： 用于神经网络的输出层。

代码实现：

import numpy as np
 
z = np.array([1.0, 2.0, 3.0])
softmax = np.exp(z) / np.sum(np.exp(z))
print(f"Softmax: {softmax}")  # 输出: [0.09003057 0.24472847 0.66524096]

注意力机制 (Attention Mechanism)

公式：

\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{Q K^T}{\sqrt{d_k}} \right) V

说明： 注意力机制基于查询 $Q$ 和键 $K$ 之间的相似性计算值 $V$ 的加权和，并按 $\sqrt{d_k}$ 进行缩放。

实际应用： 驱动 NLP 及其他领域的 Transformer 模型。

代码实现：

import torch
 
def attention(Q, K, V):
    d_k = Q.size(-1)
    scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))
    attn = torch.softmax(scores, dim=-1)
    return torch.matmul(attn, V)
 
Q = torch.tensor([[1., 0.], [0., 1.]])
K = torch.tensor([[1., 1.], [0., 1.]])
V = torch.tensor([[0., 1.], [1., 0.]])
output = attention(Q, K, V)
print(output)

总结

本博文探讨了机器学习中最关键的公式，从基础的概率论和线性代数到扩散模型和注意力机制等高级概念。通过理论解释、实践实现和可视化思考，你现在拥有了一个理解和应用机器学习数学的全面资源。如果有人问起机器学习的核心数学，就把他们引向这里——他们将在一处学到 95% 所需的知识！

机器学习核心公式全攻略

动机

简介

概率与信息论

贝叶斯定理

熵 (Entropy)

联合概率与条件概率

KL 散度 (Kullback-Leibler Divergence)

交叉熵 (Cross-Entropy)

线性代数

线性变换

特征值与特征向量

奇异值分解 (SVD)

优化

梯度下降

反向传播

损失函数

均方误差 (MSE)

交叉熵损失

高级机器学习概念

扩散过程 (Diffusion Process)

卷积运算 (Convolution Operation)

Softmax 函数

注意力机制 (Attention Mechanism)

总结

延伸阅读