TFHE-rs repo

TFHE-rs深度解析之二：数学结构和密文类型

Chuck Chen
 · 
分类： [密码学]
标签： #全同态加密 #隐私保护 #TFHE
TFHE-rs系列

TFHE算法回顾

数学结构

在深入了解密文类型之前，我们需要明确 TFHE-rs 所依赖的底层数学域。

1. 实数环面 (Real Torus, T\mathbb{T})

TFHE 方案的一个显著特点是它定义在实数环面 T=R/Z\mathbb{T} = \mathbb{R}/\mathbb{Z} 上。这意味着所有的数据和运算都是模 1 的实数。

  • 相位编码: 消息通常被编码在环面元素的“相位”中。
  • 离散化: 在 TFHE-rs 的工程实现中，为了在计算机上高效运行，实数环面被离散化并映射到整数环 Zq\mathbb{Z}_q 上，其中 qq 通常取 2322^{32} 或 2642^{64}。
    • T≅Z/232Z\mathbb{T} \cong \mathbb{Z}/2^{32}\mathbb{Z} (对应 u32)
    • T≅Z/264Z\mathbb{T} \cong \mathbb{Z}/2^{64}\mathbb{Z} (对应 u64)
    • 这种映射利用了计算机原生整数溢出的特性，使得模运算（模 2322^{32} 或 2642^{64}）可以自动且高效地完成，无需额外的取模指令。

2. 多项式环 (Polynomial Ring, R\mathcal{R})

为了支持更高级的操作（如打包和盲旋转），TFHE 扩展到了多项式环 R=Zq[X]/(XN+1)\mathcal{R} = \mathbb{Z}_q[X]/(X^N+1)。

  • 结构: 这里的元素是阶数小于 NN 的多项式，系数来自 Zq\mathbb{Z}_q。NN 通常是 2 的幂（如 1024 或 2048）。
  • 模运算: 多项式乘法是模 XN+1X^N+1 进行的，这被称为负循环卷积（Negacyclic Convolution）。
  • FFT/NTT 加速: 这种多项式结构允许我们使用快速傅里叶变换（FFT）或数论变换（NTT）来极大地加速多项式乘法运算，这是实现高效自举的关键。

核心密文类型

TFHE-rs 的高效性很大程度上归功于其使用的三种主要密文类型及其泛化形式：LWE、GLWE 和 GGSW。理解这些类型的层级关系和相互作用是理解 TFHE 算法的关键。

1. LWE 密文 (LWE Ciphertext)

LWE (Learning With Errors) 是最基础的密文类型。 在 TFHE-rs 中，我们使用的是定义在环面 T=R/Z\mathbb{T} = \mathbb{R}/\mathbb{Z} 上的 LWE，即 TLWE。但在工程实现中，环面被映射到模 2322^{32} 或 2642^{64} 的整数环上。

  • 结构：在选定密钥s∈Zqn\mathbf{s} \in \mathbb{Z}_q^n和随机采样向量a∈Zqna \in \mathbb{Z}_q^n下，消息mm的LWE密文是 LWEs(m)=(a,b)∈Zqn×Zq\mathsf{LWE}_\mathbf{s}(m) = (\mathbf{a}, b) \in \mathbb{Z}_q^n \times \mathbb{Z}_q 其中， b=⟨a,s⟩+Δ⋅m+eb = \langle \mathbf{a}, \mathbf{s} \rangle + \Delta \cdot m + e Δ\Delta 是缩放因子，mm 是消息，ee 是高斯误差。
  • 用途: 用于加密单个标量值（如布尔位或整数）。它是可编程自举（PBS）的输入和输出格式。

2. GLWE 密文 (General LWE Ciphertext)

GLWE 是 LWE 和 RLWE (Ring LWE) 的统一泛化形式。它定义在多项式环 R=Zq[X]/(XN+1)\mathcal{R} = \mathbb{Z}_q[X]/(X^N+1) 上。

  • 参数: 维度 kk 和多项式阶数 NN。
  • 结构: 一个 GLWE 密文包含 kk 个多项式掩码和一个多项式 GLWE(m)=CT=(A0,…,Ak−1,B)∈Rq,Nk+1\mathsf{GLWE}(m) = \mathsf{CT} = (A_0, \dots, A_{k-1}, B) \in \mathcal{R}^{k+1}_{q,N} 其中， B=∑i=0k−1Ai⋅Si+Δ⋅M+E∈Rq,NB = \sum_{i=0}^{k-1} A_i \cdot S_i + \Delta \cdot M + E \in \mathcal{R}_{q,N}
  • 统一性:
    • 当 N=1N=1 时，GLWE 退化为标准的 LWE（此时 kk 即为 LWE 的维度 nn）。
    • 当 k=1k=1 时，GLWE 即为 RLWE。
  • 用途: 用于加密多项式。在自举过程中，核心的累加器（Accumulator） 就是一个 GLWE 密文。它可以利用 SIMD 特性打包多个数据，或者用于高效的多项式运算。

3. GLev 密文 (General Leveled Ciphertext)

在介绍 GGSW 之前，需要引入 GLev 密文。这是一个中间结构，主要用于处理同态运算中的噪声管理。

  • 原理: 为了在乘法运算中控制噪声增长，我们需要使用Gadget分解（Gadget Decomposition）。
  • 结构: 一个 GLev 密文实际上是一个 GLWE 密文的列表（List）。每个 GLWE 密文都加密相同的消息 MM，但使用了不同的缩放因子（通常是 1β,1β2,…,1βℓ\frac{1}{\beta}, \frac{1}{\beta^2}, \dots, \frac{1}{\beta^\ell}）。
  • 用途: 它是构建 GGSW 密文的基础组件。

4. GGSW 密文 (General GSW Ciphertext)

GGSW 是 GSW 和 TGSW (Torus GSW) / RGSW 的泛化形式。

  • GSW 基础: Gentry-Sahai-Waters (GSW) 方案引入了基于矩阵的加密方式。其核心思想是近似特征向量（Approximate Eigenvector）：密文矩阵 CC 乘以私钥向量 S\mathbf{S} 约等于消息 μ\mu 乘以私钥向量。 C⋅S≈μ⋅SC \cdot \mathbf{S} \approx \mu \cdot \mathbf{S} 这使得同态加法和乘法可以转化为简单的矩阵加法和乘法，且噪声增长非常缓慢。
  • 结构: 一个 GGSW 密文可以被看作是一个 GLev 密文的列表。具体来说，它是一个矩阵，其中的每一行都是一个 GLev 密文。
    • 矩阵的行数通常为 (k+1)⋅ℓ(k+1) \cdot \ell，其中 ℓ\ell 是分解的层级数。
  • 统一性:
    • 当 N=1N=1 时，退化为标准的 GSW。
    • 当 k=1k=1 时，即为 RGSW (或 TGSW)。
  • 外部积 (External Product): 这是 TFHE 中最重要的运算之一，记为 ⊙\odot。 GGSW⊙GLWE→GLWE\text{GGSW} \odot \text{GLWE} \rightarrow \text{GLWE} 它允许我们将一个 GGSW 密文（通常代表控制位或权重）乘到一个 GLWE 密文上，且输出仍然是一个 GLWE 密文。在自举的盲旋转（Blind Rotation）步骤中，CMUX 门就是通过外部积实现的。

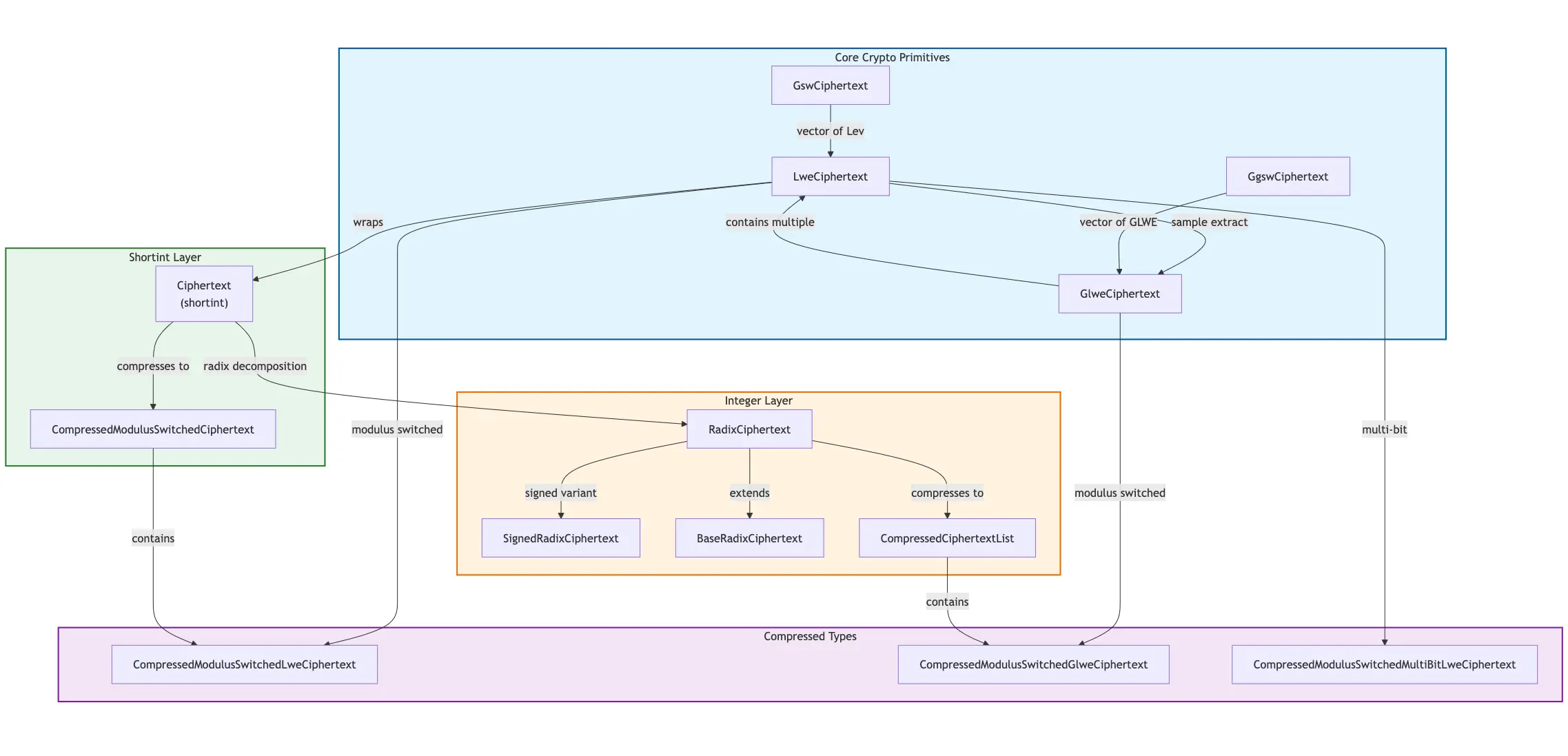
主要密文类型的转换

按照分层架构，TFHE-rs中主要的密文类型包括：

  • 核心密码层中，有最基础的LWE加密的LweCiphertext、推广到多项式环上的GlweCiphertext、GSW加密的GswCiphertext、推广到多项式环上的GgswCiphertext；
  • 应用层中，包括shortint模块中LweCiphertext及包含额外元信息的Ciphertext（也是最基础的类型）和integer模块中包含多个shortint块的RadixCiphertext；
  • 一些存储和传输的压缩类型，如CompressedModulusSwitchedCiphertext和对应的GPU上的类型CudaCompressedCiphertextList。

TFHE-rs主要密文类型的转换关系

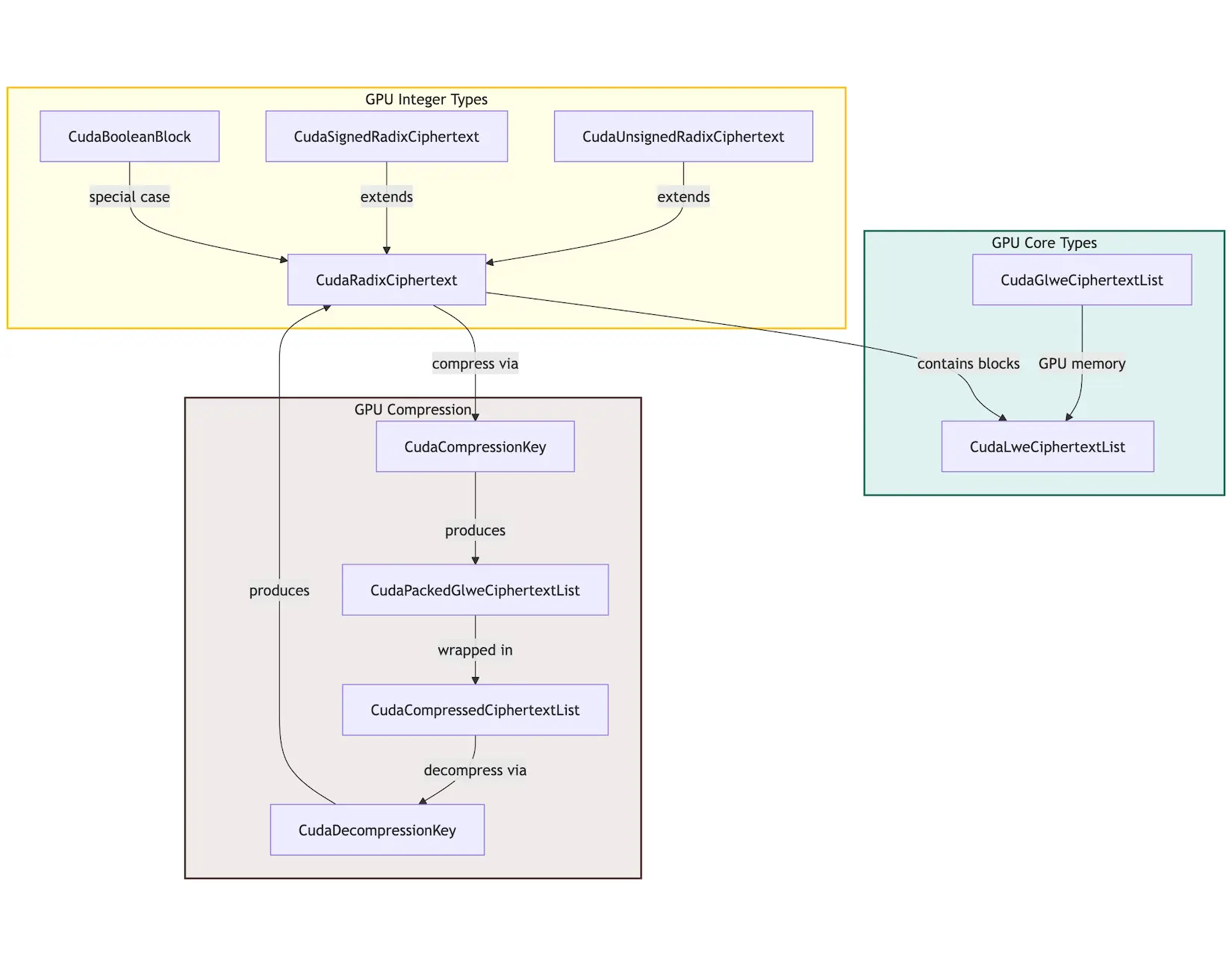
除上述类型之外，在GPU实现中还有特定的类型：CudaGlweCiphertextList便于高效的显存管理和CudaRadixCiphertext支持基本的整数密文操作。

TFHE-rs GPU密文类型的转换关系

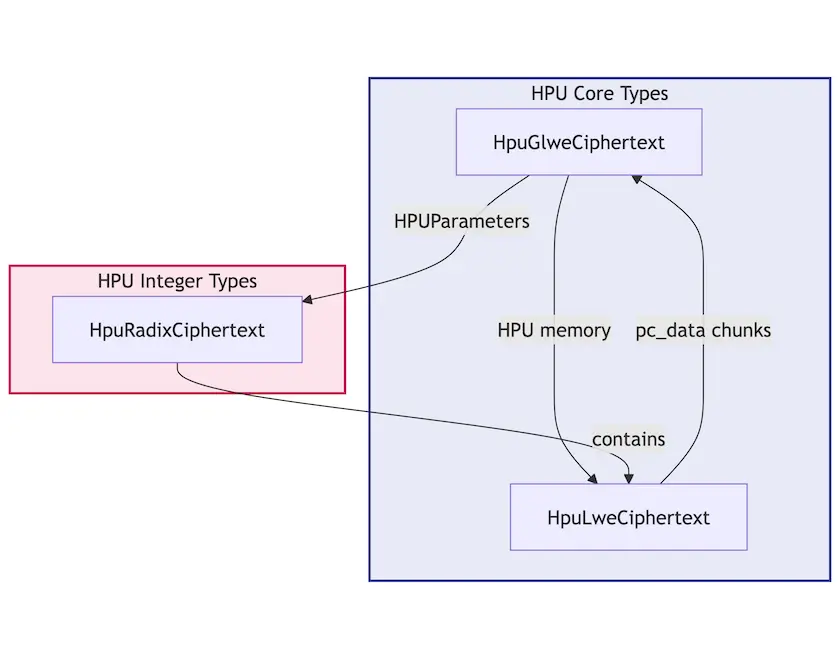
于此类似，HPU上也定义了专用类型：HpuGlweCiphertext分块密文数据和HpuLweCiphertext映射到特定内存的密文。

TFHE-rs HPU密文类型的转换关系

简化的GLWE加解密示例

为了更好地理解上述概念，我们来看一个使用不安全的小参数进行的 GLWE 加密演练（来源于 Zama 的官方文档）。

1. 参数设置 选择模数 q=64q = 64（用于密文计算），消息模数 p=4p = 4（消息空间大小），缩放因子 Δ=q/p=64/4=16\Delta = q/p = 64/4 = 16，多项式阶数 N=4N = 4，GLWE 维度 k=2k = 2

2. 密钥生成 私钥 SS 由两个系数为Z2\mathbb{Z}_2上元素（即0或1）的多项式组成：

S⃗=(S0,S1)=(0+1X+1X2+0X3,1+0X+1X2+1X3)∈R2\vec{S} = (S_0, S_1) = (0 + 1X + 1X^2 + 0X^3, 1 + 0X + 1X^2 + 1X^3) \in \mathcal{R}^2

3. 消息编码 我们要加密的消息 MM 是一个多项式，系数在Zp\mathbb{Z}_p即{−2,−1,0,1}\{-2, -1, 0, 1\} 中选择。例如M=−2+1X+0X2−1X3∈RpM = -2 + 1X + 0X^2 - 1X^3 \in \mathcal{R}_p，那么编码后的消息：

Δ⋅M=−32+16X+0X2−16X3∈Rq\Delta \cdot M = -32 + 16X + 0X^2 - 16X^3 \in \mathcal{R}_q

4. 加密过程

  • 采样掩码: 随机生成包含两个多项式的向量A⃗\vec{A}，例如取

    A⃗=(A0,A1)=(17−2X−24X2+9X3,−14+0X−1X2+21X3)∈Rq2\begin{align*} \vec{A} &= (A_0, A_1) \\ &= (17 - 2X - 24X^2 + 9X^3, -14 + 0X - 1X^2 + 21X^3) \in \mathcal{R}_q^2 \end{align*}

  • 采样误差: 生成一个小的高斯误差多项式 EE，例如

    E=−1+1X+0X2+1X3∈RqE = -1 + 1X + 0X^2 + 1X^3 \in \mathcal{R}_q

  • 计算密文中第三个多项式，B=A0⋅S0+A1⋅S1+Δ⋅M+E∈RqB = A_0 \cdot S_0 + A_1 \cdot S_1 + \Delta \cdot M + E \in \mathcal{R}_q。

    经过Rq=Zq/[X4+1]\mathcal{R}_q = \mathbb{Z}_q / [X^4 + 1]上多项式乘法和模运算（注意 X4≡−1X^4 \equiv -1），我们得到：

    A0⋅S0=(17−2X−24X2+9X3)(0+1X+1X2+0X3)=24+8X+15X2−26X3A1⋅S1=(−14+0X−1X2+21X3)(1+0X+1X2+1X3)=−13−20X+29X2+7X3\begin{align*} A_0 \cdot S_0 &= (17 - 2X - 24X^2 + 9X^3)(0 + 1X + 1X^2 + 0X^3) \\ &= 24 + 8X + 15X^2 - 26X^3 \\ A_1 \cdot S_1 &= (-14 + 0X - 1X^2 + 21X^3)(1 + 0X + 1X^2 + 1X^3) \\ &=-13 - 20X + 29X^2 + 7X^3 \end{align*}

    最终

    B=24+8X+15X2−26X3+(−13−20X+29X2+7X3)+(−32+16X+0X2−16X3)+(−1+1X+0X2+1X3)=−21+5X−20X2+30X3\begin{align*} B =& 24 + 8X + 15X^2 - 26X^3 + (-13 - 20X + 29X^2 + 7X^3) \\ &+(-32 + 16X + 0X^2 - 16X^3) + (-1 + 1X + 0X^2 + 1X^3) \\ =& -21 + 5X - 20X^2 + 30X^3 \end{align*}

    最终的密文为 (A0,A1,B)(A_0, A_1, B)。

5. 解密过程

  • 计算带误差编码消息：计算B−(A0⋅S0+A1⋅S1)B - (A_0 \cdot S_0 + A_1 \cdot S_1)。

    Δ⋅M+E=B−(A0⋅S0+A1⋅S1)=−21+5X−20X2+30X3−(24+8X+15X2−26X3)−(−13−20X+29X2+7X3)=−32+23X+0X2−15X3\begin{align*} \Delta \cdot M + E =& B - (A_0 \cdot S_0 + A_1 \cdot S_1) \\ =& -21 + 5X - 20X^2 + 30X^3 - (24 + 8X + 15X^2 - 26X^3) \\ &- (-13 - 20X + 29X^2 + 7X^3) \\ =& -32 + 23X + 0X^2 - 15X^3 \end{align*}

  • 恢复消息：为从上一步的结果 Δ⋅M+E\Delta \cdot M + E恢复消息，我们将每一项系数除以 Δ=16\Delta = 16 并四舍五入：

    • 常数项: −32/16=2→2≡−2(mod4)-32/16 = 2 \to 2 \equiv -2 \pmod 4
    • XX 项: 23/16≈1.43→123/16 \approx 1.43 \to 1
    • X2X^2 项: 0/16=0→00/16 = 0 \to 0
    • X3X^3 项: −15/16≈−0.94→−1-15/16 \approx -0.94 \to -1

    恢复出的消息 M′=−2+1X+0X2−1X3M' = -2 + 1X + 0X^2 - 1X^3，与原消息MM一致。